Geoestatística aplicada a agricultura de precisão
Geoestatística aplicada ao mapeamento da fertilidade do solo
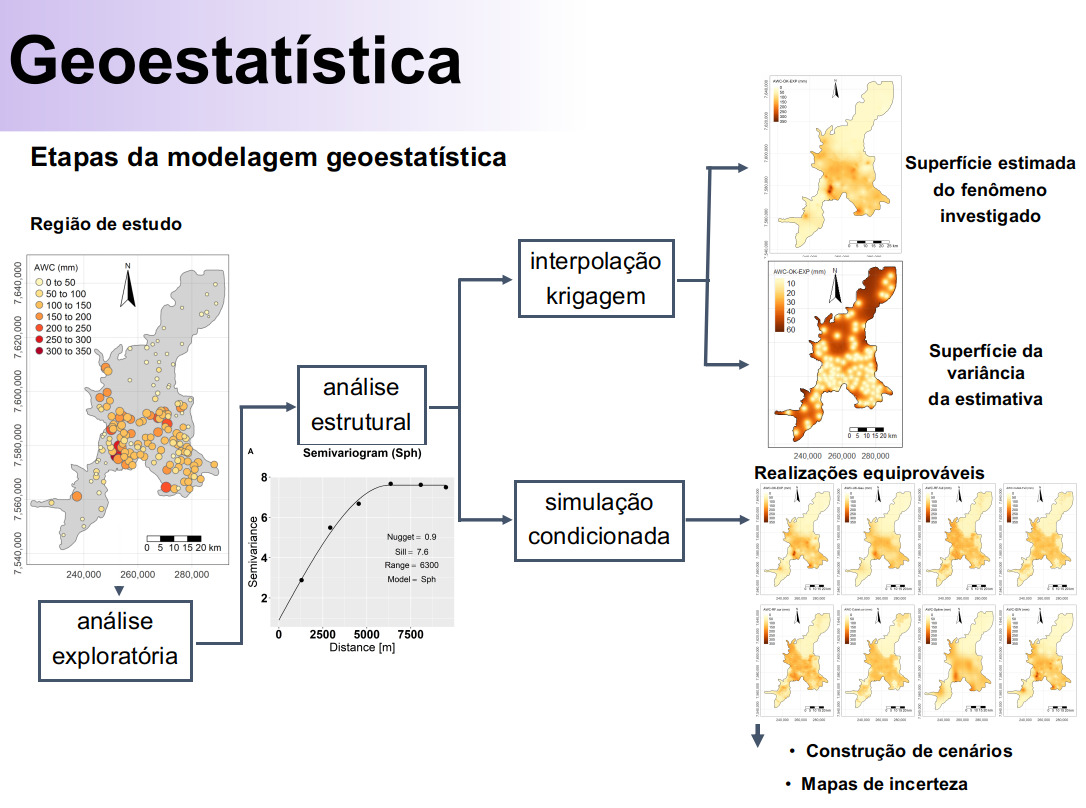 Image credit: Elias
Image credit: Elias
Introdução
A geoestatística como conhecemos hoje começou com os trabalhos de Krige (1951). Para ele somente a informação dada pela variância não seria suficiente para explicar o fenômeno em estudo. Para tal, seria necessário levar em consideração a distância entre as observações. A partir daí surge o conceito da geoestatística, que leva em consideração a localização geográfica e a dependência espacial entre amostras.
Matheron (1963) e Matheron (1971) , baseado-se nas observações de Krige, desenvolveu a teoria das variáveis regionalizadas. Uma variável regionalizada é uma função numérica com distribuição espacial, que varia de um ponto a outro com continuidade aparente, mas cujas variações não podem ser representadas por uma função matemática simples.
A teoria das variáveis regionalizadas pressupõe que a variação de uma variável pode ser expressa pela soma de três componentes: a) uma componente estrutural, associada a um valor médio constante ou a uma tendência constante; b) uma componente aleatória, espacialmente correlacionada; e c) um ruído aleatório ou erro residual.
Assim um valor da variável Z em um local x é dado por:
\[ Z(x)=m(x)+\varepsilon′(x)+\varepsilon′′ \] onde: m(x) é uma função determinística que descreve a componente estrutural de Z em x; ε′(x) é um termo estocástico, que varia localmente e depende espacialmente de m(x); ε′′ é um ruído aleatório não correlacionado, com distribuição normal com média zero e variância σ2
Um dos modelos mais simplistas dessa variação é o calculado pelo inverso do quadrado da distância que assume que qualquer atributo do solo varia a taxa fixa do inverso da distância, o que na prática não é bem verdade, mas em muitos casos esse modelo atende a necessidade.
Variograma
O variograma é uma ferramenta básica de suporte às técnicas de krigagem, que permite representar quantitativamente a variação de um fenômeno regionalizado no espaço. Considere duas variáveis regionalizadas, X e Y, onde X = Z(x) e Y = Z(x+h). Neste caso, referem-se ao mesmo atributo medido em duas posições diferentes.
O nível de dependência entre essas duas variáveis regionalizadas, X e Y, é representado pelo variograma, 2γ(h), o qual é definido como a esperança matemática do quadrado da diferença entre os valores de pontos no espaço, separados pelo vetor distância h, isto é,
\[ 2γ(h) = E{[Z(x)-Z(x+h)] 2 } = Var[Z(x)-Z(x+h)]\] Através de uma amostra z(x i ), i=1, 2, /home/elias/MEGA/Geo., n, o variograma pode ser estimado por
\[ 2Ŷ(h)=\frac{1}{N(h)}\sum^{N(h)}_{i=1}[Z(x_i)-Z(X_i+h)]²\] onde: - 2Ŷ(h) - é o variograma estimado; - N(h) - é o número de pares de valores medidos, z(xi) e z(xi+h), separados por um vetor distância h; - z(xi) e z(xi +h), - são valores da i-ésima observação da variável regionalizada, coletados nos pontos xi e xi+h (i = 1, /home/elias/MEGA/Geo., n), separados pelo vetor h.
Parâmetros do semivariograma
O seu padrão representa o que, intuitivamente, se espera de dados de campo, isto é, que as diferenças {Z(xi) - Z(xi+h)} decresçam à medida que h, a distância que os separa decresce. É esperado que observações mais próximas geograficamente tenham um comportamento mais semelhante entre si do que aquelas separadas por maiores distâncias. Desta maneira, é esperado que γ(h) aumente com a distância h.

Figure 1: Exemplo de Semivariograma.
- Alcance (a) (range): distância dentro da qual as amostras apresentam-se correlacionadas espacialmente.
- Patamar (C) (sill): é o valor do semivariograma correspondente a seu alcance (a).Deste ponto em diante, considera-se que não existe mais dependência espacial entre as amostras, porque a variância da diferença entre pares de amostras (Var[Z(x) - Z(x+h)]) torna-se invariante com a distância. Pode ser definido também como variância total.
- Efeito Pepita (C0)(nugget): A medida que h tende para 0 (zero), g(h) se aproxima de um valor positivo chamado Efeito Pepita (C0), que revela a descontinuidade do semivariograma para distâncias menores do que a menor distância entre as amostras, pode ser definido também como variância residual.
Estrutura espacial local
Se consideramos as coordenadas de cada ponto é possível obervar uma tendência regional ou uma estrutura local dos dados, umas das formas mais simples de observar a dependência espacial é atraves de plot espacial dos valores observados.
Agora analisamos a ideia de dependência espacial local: “mais perto no espaço geográfico implica mais perto no espaço de atributos”. Isso pode ser verdade ou não;e se for verdade, o intervalo de dependência irá variar, dependendo do processo físico que produziu o atributo que está sendo investigado, nesse caso o teor de argila do solo.
O conceito fundamental é que deve ser entendido nesse contexto é a autocorrelação espacial: um valor de atributo pode ser correlacionado consigo mesmo, com a força da correlação dependendo da distância de separação (e possivelmente na direção). Isso deve ser evidente como uma relação entre a distância de separação e correlação; para análisar essas relações usamos o conceito de semivariância como já mencionado quando apresentado o semivariograma.Esse análise é feita com base no número de pares possíveis do dataset que pode ser determinado por (n × (n - 1))/2 pares.
Quando fazemos o variograma experimental dos teores de COT, é calculado as semivariâncias médias dos pares de pontos versus distância média(também conhecido como “lag”), com cumprimento definido pelo usuário, e distância máxima de busca cutoff.
Modelos teóricos
Selecionar uma forma de modelo é uma arte; a melhor maneira é a partir do conhecimento do processo espacial e da forma como o modelo se ajusta ao semivariograma esperimental.
A função vgm especifica um modelo de variograma. No conjunto anterior nós estimamos esses parâmetros observando o variograma empírico, então os fornecemos como parâmetros do modelo. Observe que para cada modelo há um conjunto de parâmetro que melhor se ajusta. Para fins de exemplo vamos testar os 3 principais modelos, neles teremos que ajustar o “parcial sill” (contribuição) psill que é o patamar menos o efeito pepita (nugget) e o alcance (range)
Possíveis modelos no pacote gstat
library(gstat)
library(sp)
library(readxl)
library(tmap)
library(raster)
print(show.vgms())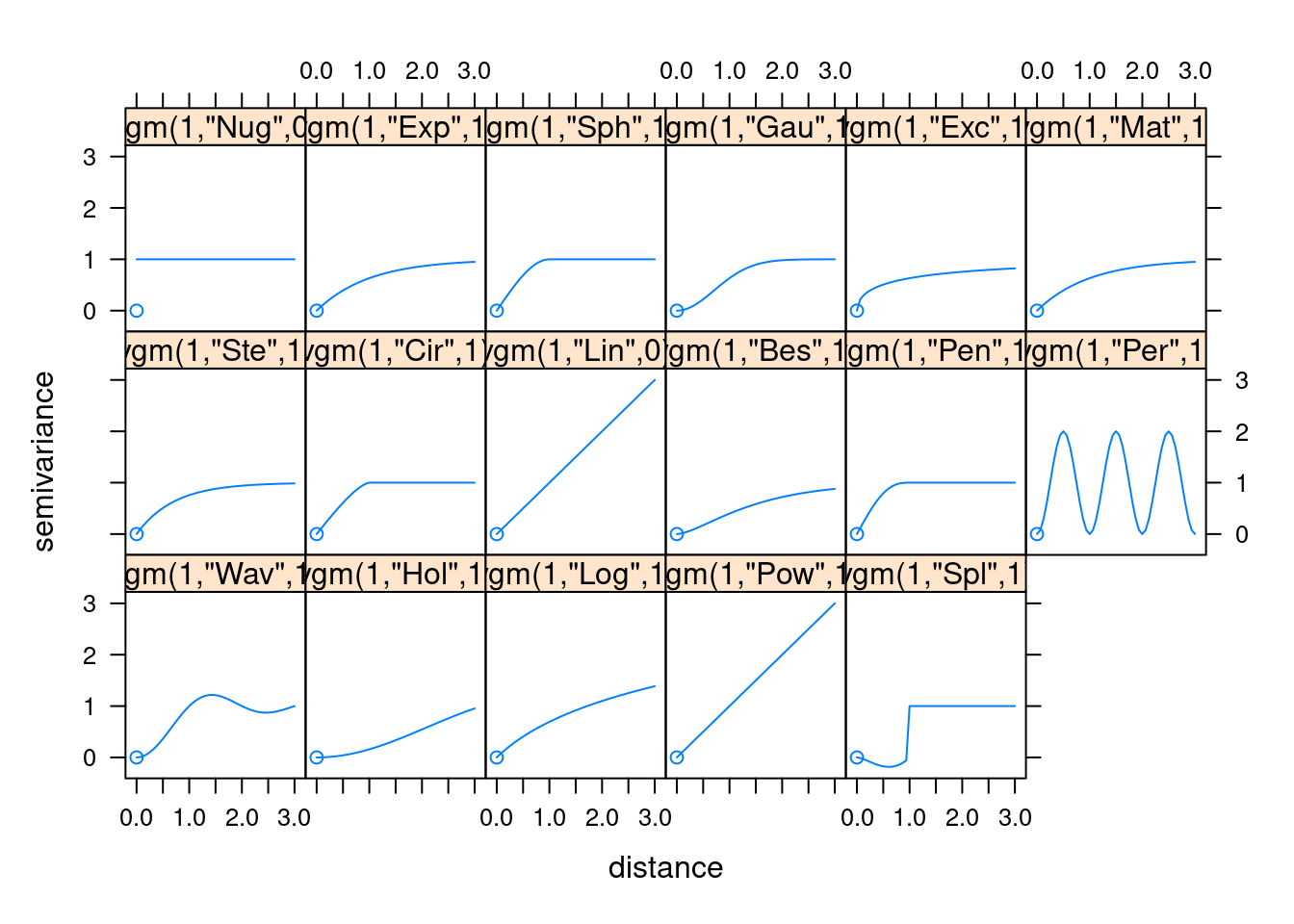
data <- read_excel("/home/elias/MEGA/Geo/data/Análises.xls",
col_types = c("numeric", "numeric", "numeric",
"numeric", "numeric", "numeric",
"numeric", "numeric", "numeric",
"numeric"))
## Definindo o sistema de projeto do conjunto de dados
WGS23S = sp::CRS("+proj=utm +zone=23 +south +datum=WGS84 +units=m +no_defs +ellps=WGS84 +towgs84=0,0,0")
## Transformando o dataframe "data" em informação espacial
coordinates(data) = ~X+Y
sp::proj4string(data) = WGS23S ## Definindo sistema de coordenadas para os DADOS
plot(data)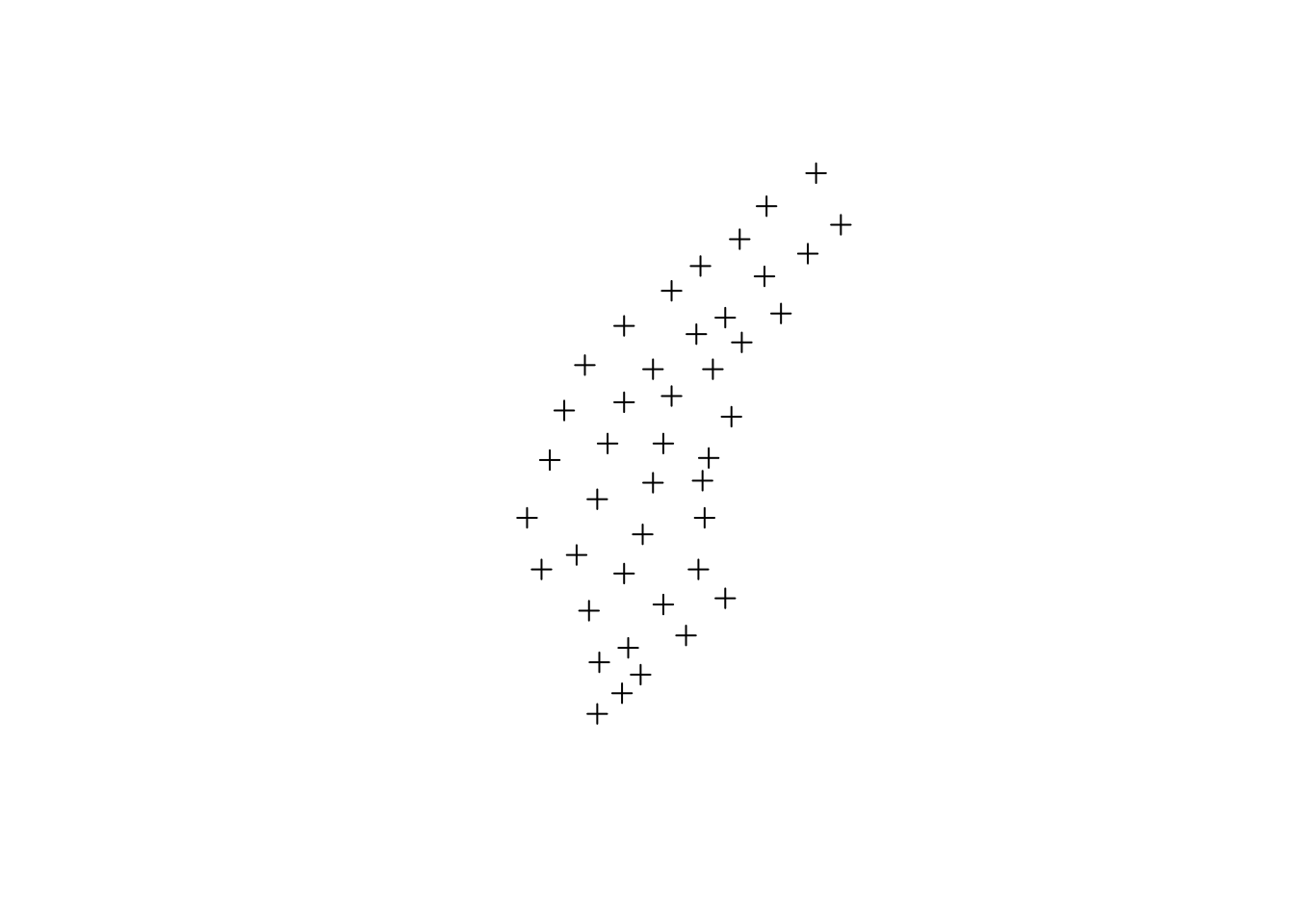
## Carregando arquivo raster para uso como grid de refer?ncia na interpolação
raster=raster::brick("/home/elias/MEGA/Geo/raster/mosaico.tif")
#plotRGB(raster, 1, 2, 3)
sp::proj4string(raster) = WGS23S
#raster=projectRaster(raster, crs = WGS23S)
#plot(raster)
## Transformando o arquivo "raster" em arquivo "SpatialPixelsDataFrame" para posterior uso como grid de referência
grid=as(raster, "SpatialPixelsDataFrame")
############### Analisando de forma qualitativa a depedência espacial)
plot(data, asp=1, cex=4*data$ADT/max(data$ADT), pch=1)## Warning in max(data$ADT): no non-missing arguments to max; returning -Inf
#############
# Aqui vamos ver de forma detalhada e didática (passo a passo) da avaliação de depedência espacial. Na prática não há necessidade de seguir todos esses passos.
n <- length(data$COT) # comprimento do conjunto de dados
n*(n-1)/2 ## Calculando o número de pares de pontos## [1] 903# Agora como exercício vamos calcular a semivariância entre os dois primeiros pontos do dataset
coordinates(data)[1,] # linha 1## X Y
## 634733 7481375coordinates(data)[2,] # linha 2## X Y
## 634745 7481350sep <- dist(coordinates(data)[1:2,]) # distância entre o ponto 1 e ponto 2
gamma <- 0.5 * (data$ADT[1] - data$ADT[2])^2 # semivariância entre o ponto 1 e ponto 2
max(dist(data@coords))*2/3 # Máxima distância entre os pontos, para limitar a distância do variograma em 2/3 da Máxima distância## [1] 188.4203min(dist(data@coords)) # minima distância entre pontos, ajuda a definir o tamanho do lag## [1] 11.40175# Variograma de núvem
variograma <- gstat::variogram(COT ~ 1, data, cloud = TRUE, cutoff = Inf)
plot(variograma, ylab = "semivariância", xlab = "distância (m)")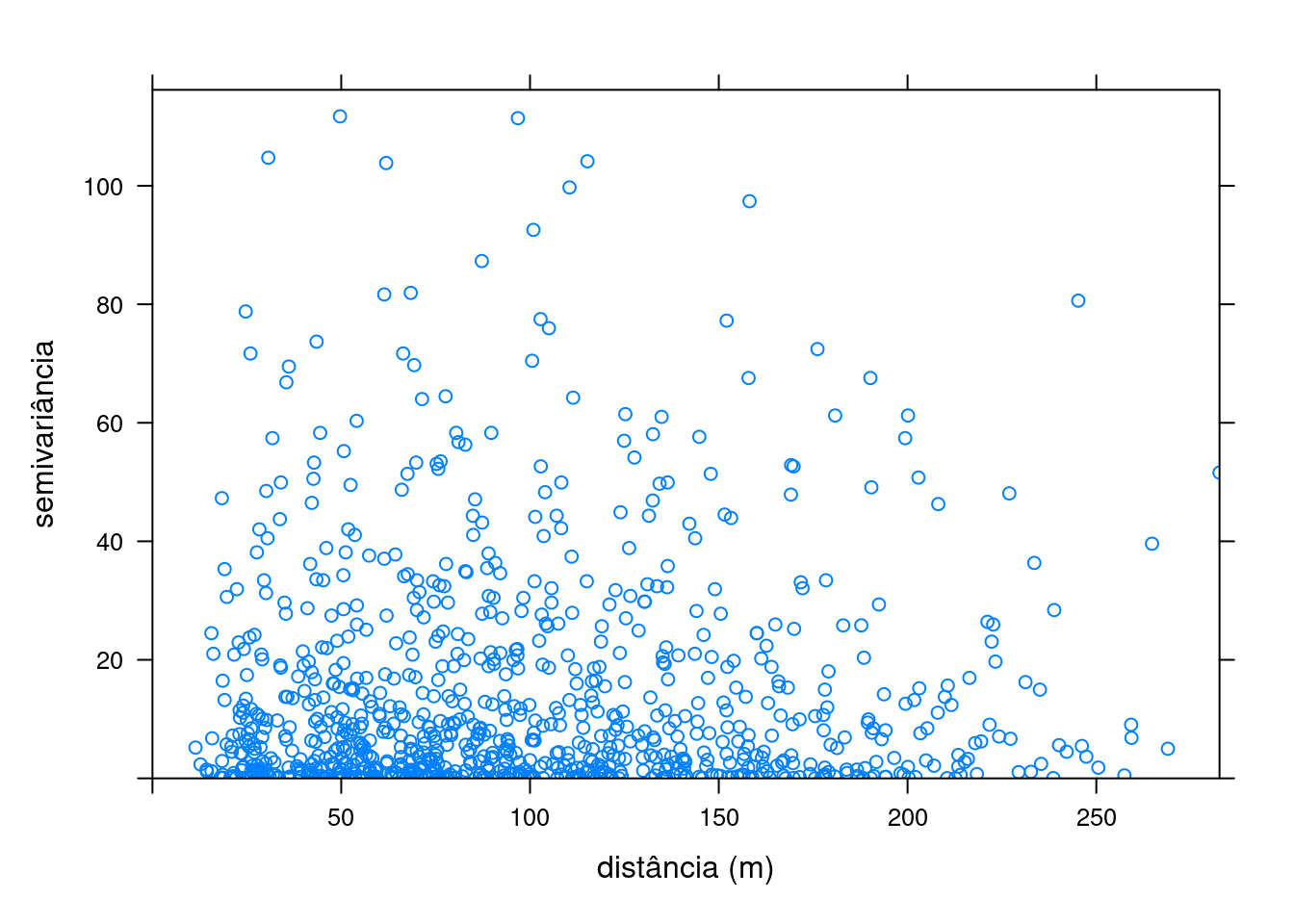
# Variograma experimental
v <- variogram(COT ~ 1, data, cutoff=90, width=7)
print(plot(v, plot.numbers=F))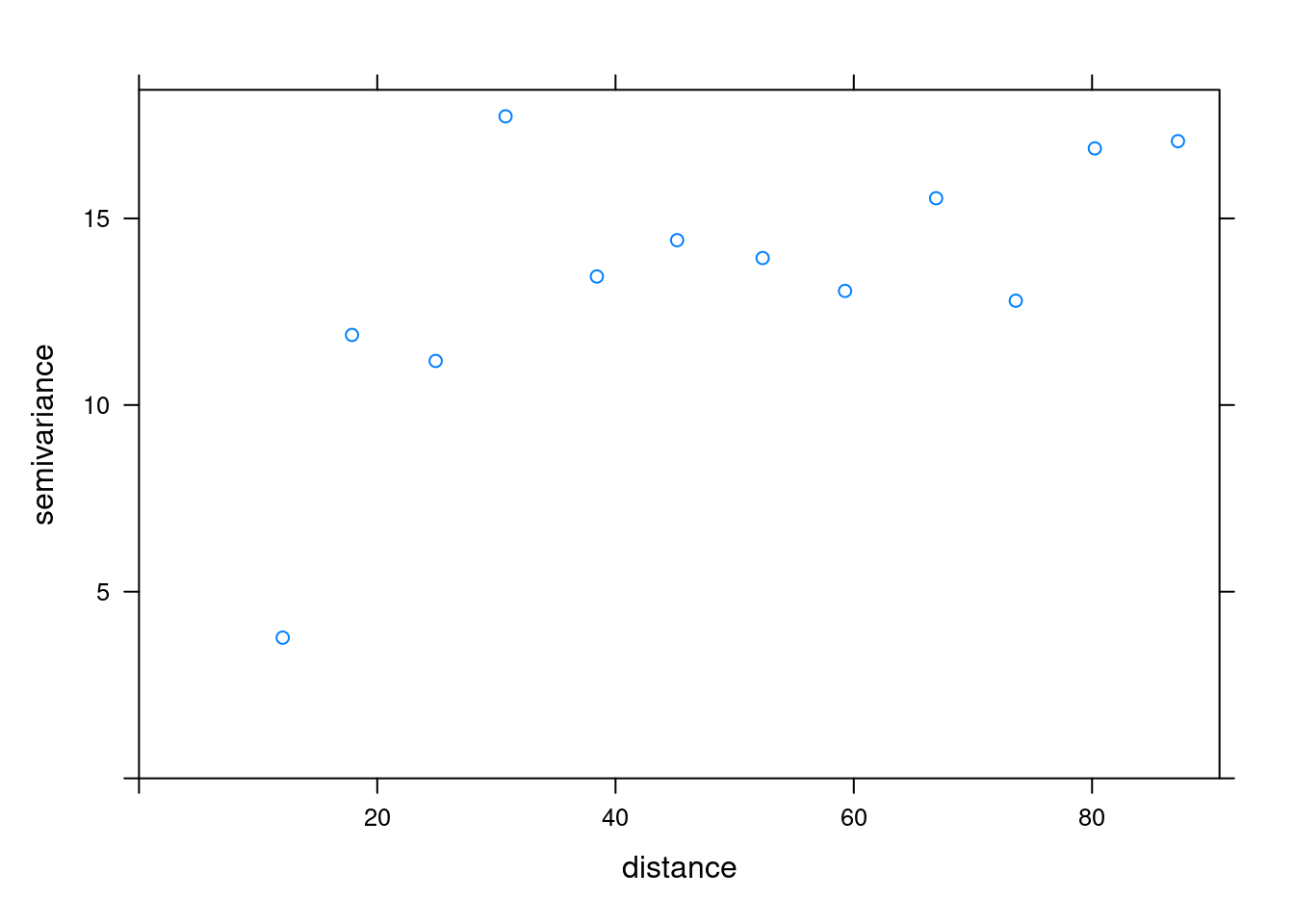
# width é o tamanho do lag (passo), ou seja, um ponto médio (uma simplificação) a cada 1800 m
# Cutoff = distância Máxima de busca que a gente viu em 2/3 é em torno de 70000 m, mas vimos que uma distância mais curta é melhor então usamos 11000
####### Alguns exemplos de possíveis modelos disponíveis em R #####
print(show.vgms())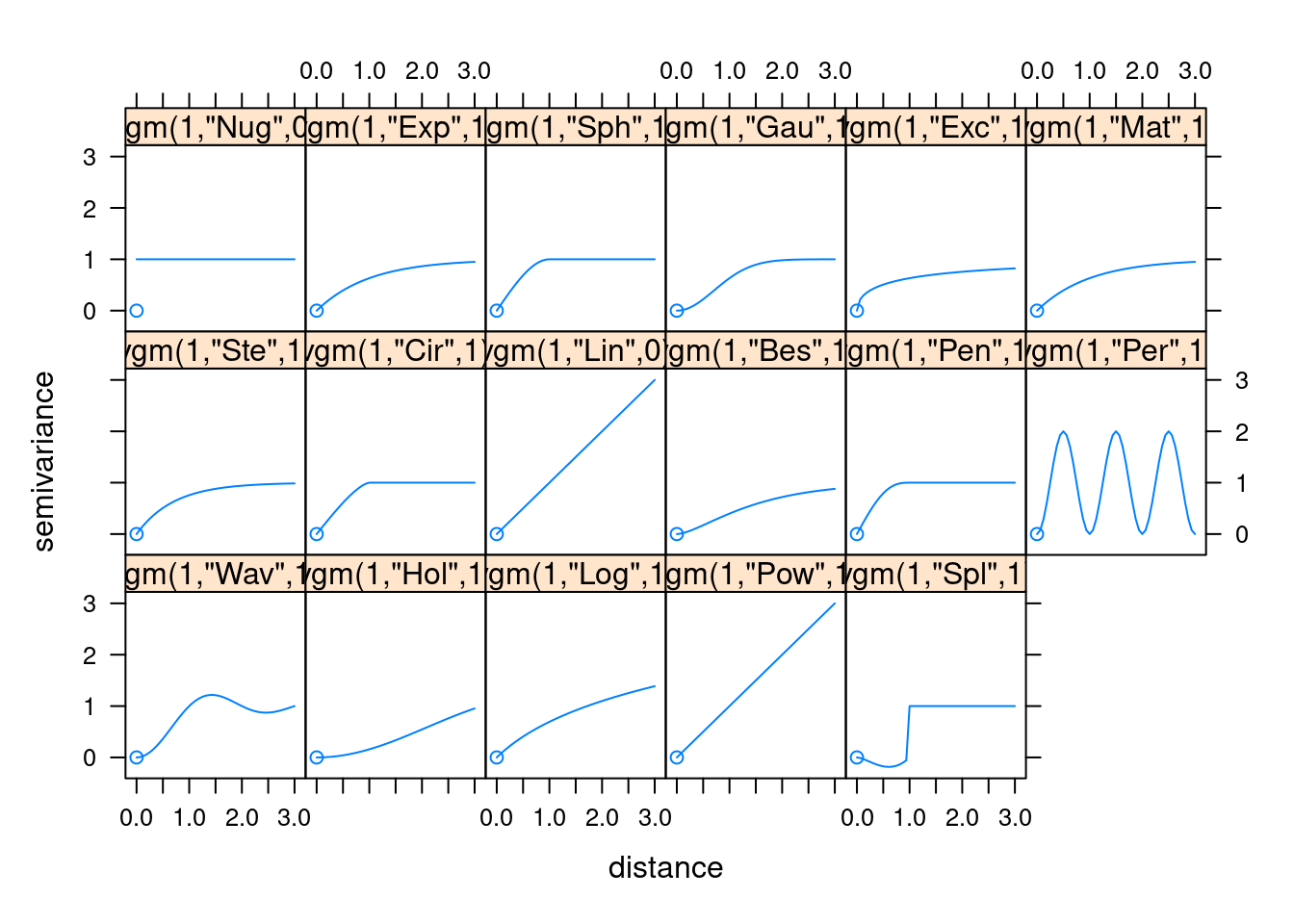
### Modelo esférico
vm1 <- vgm(psill=15, model="Sph",range=40,nugget=0)
print(plot(v, pl=F, model=vm1, main = "Esférico"))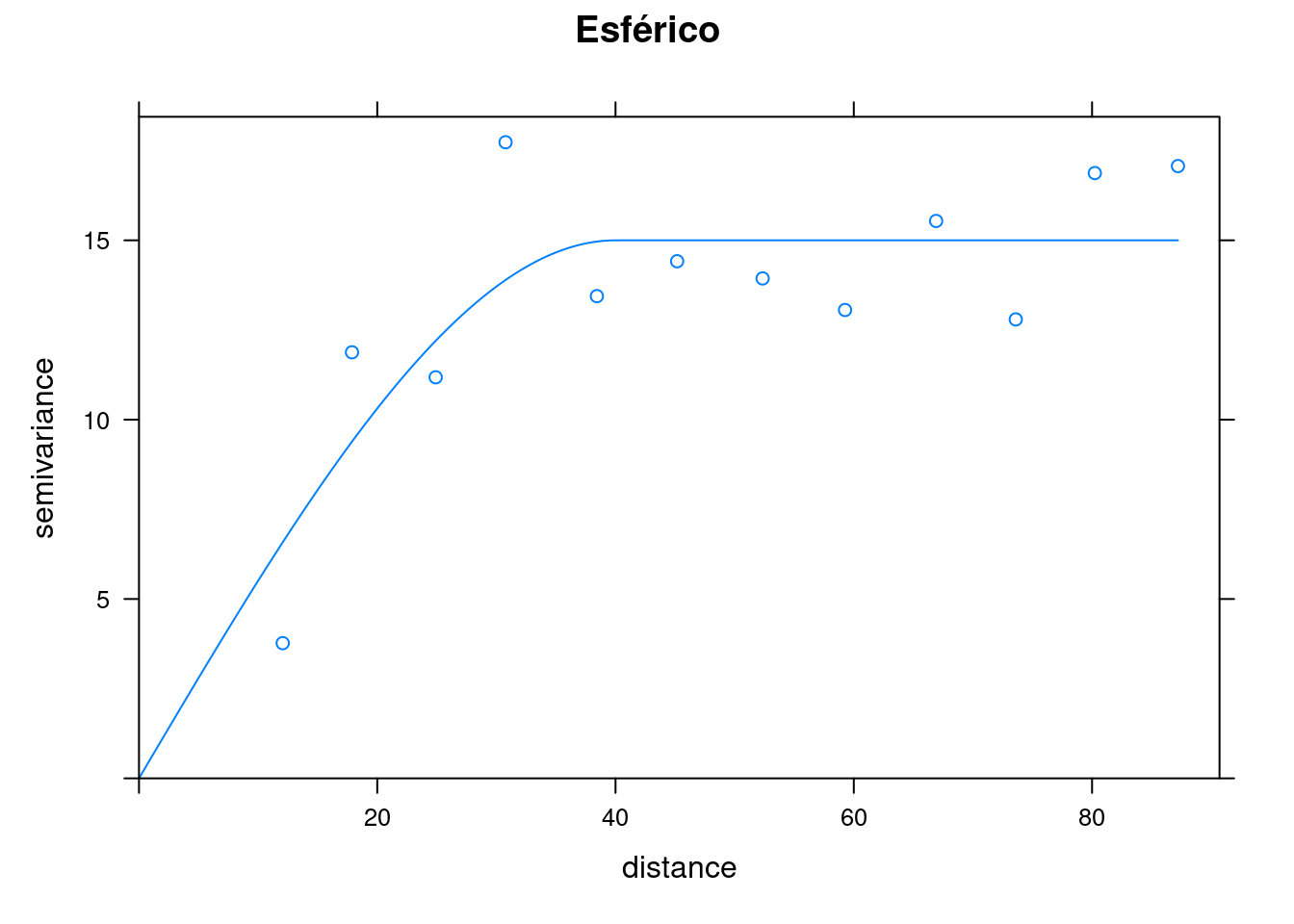
### Modelo Exponencial
vm2 <- vgm(psill=15, model="Exp",range=15,nugget=0)
print(plot(v, pl=F, model=vm2))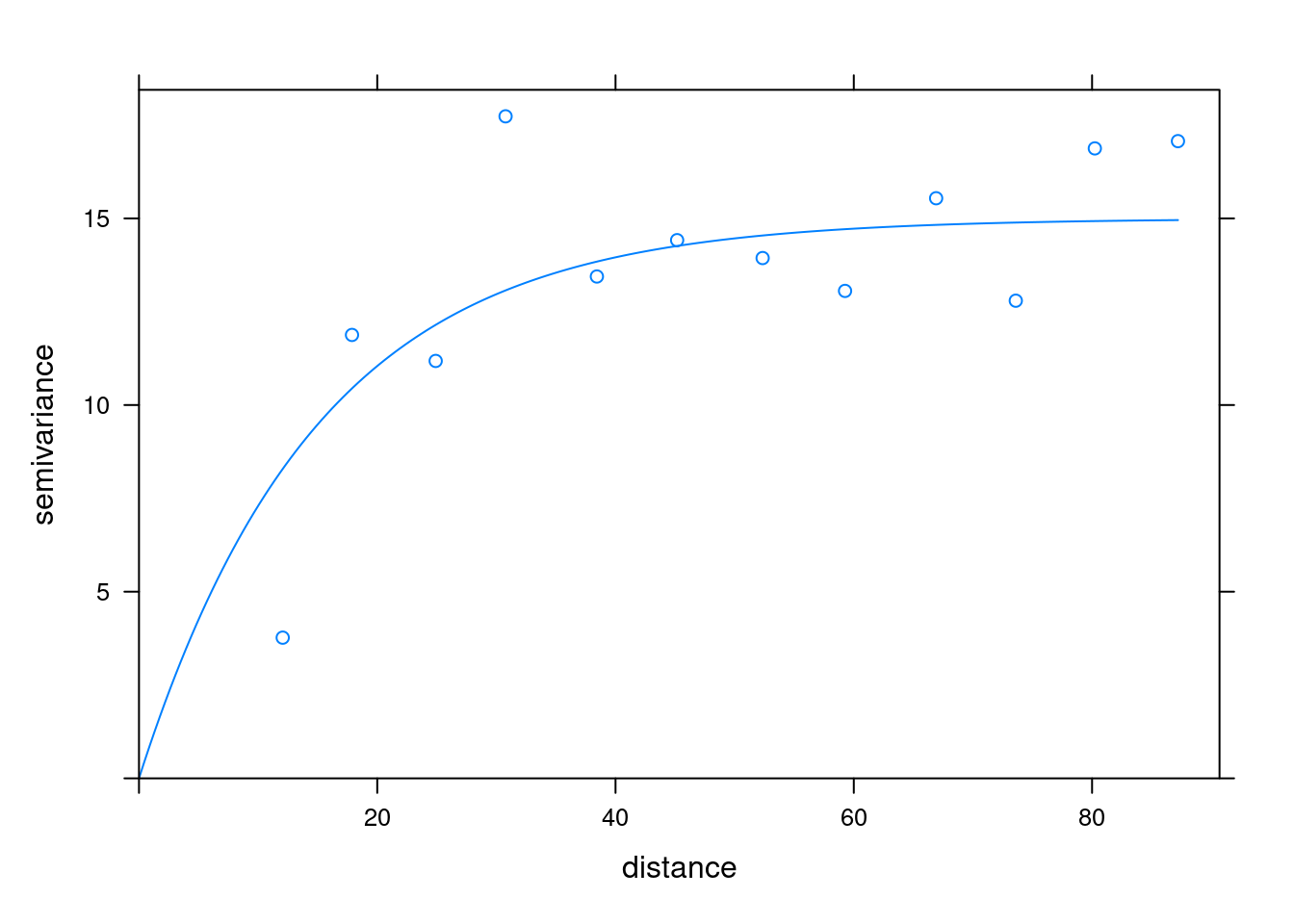
### Modelo Gaussiano
vm3 <- vgm(psill=16, model="Gau",range=20,nugget=0)
print(plot(v, pl=F, model=vm3))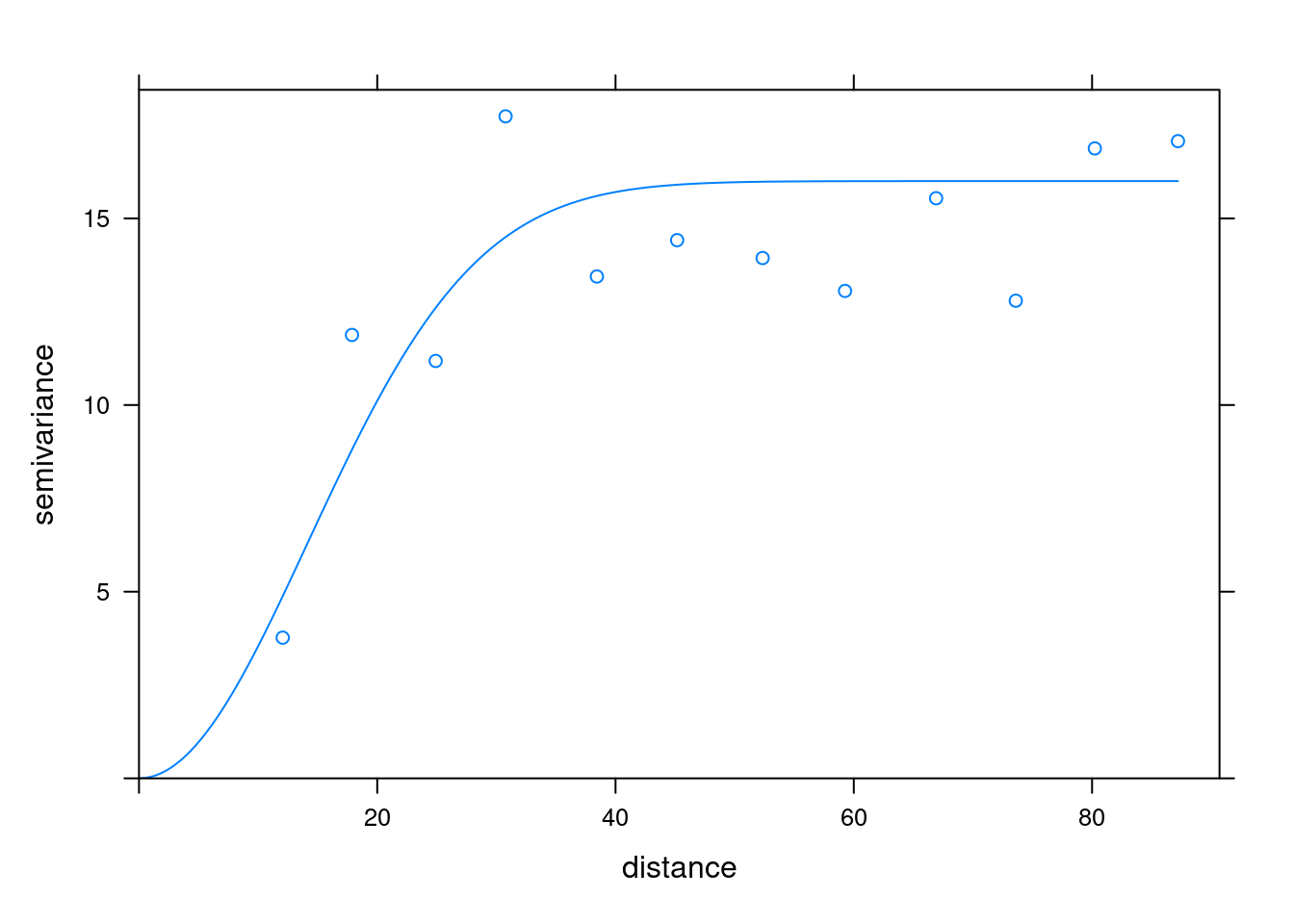
# Modelo Ajustado esférico
(vmf1 <- fit.variogram(v, vm1))## Warning in fit.variogram(v, vm1): No convergence after 200 iterations: try
## different initial values?## model psill range
## 1 Nug 0.00000 0.00000
## 2 Sph 14.66166 35.26004print(plot(v, pl=F, model=vmf1))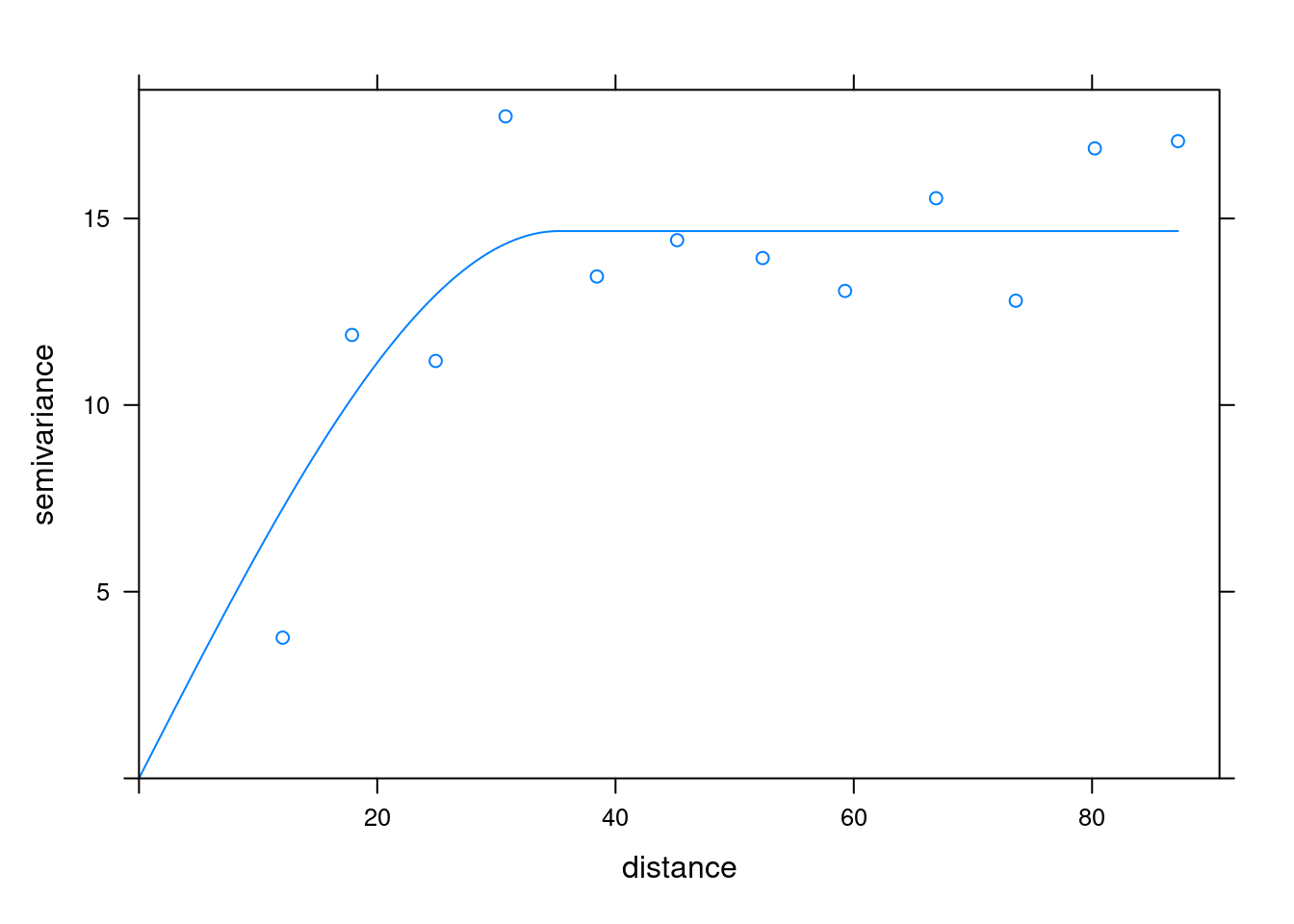
# Modelo Ajustado Exponencial
(vmf2 <- fit.variogram(v, vm2))## model psill range
## 1 Nug 0.00000 0.00000
## 2 Exp 15.34669 14.71238print(plot(v, pl=F, model=vmf2))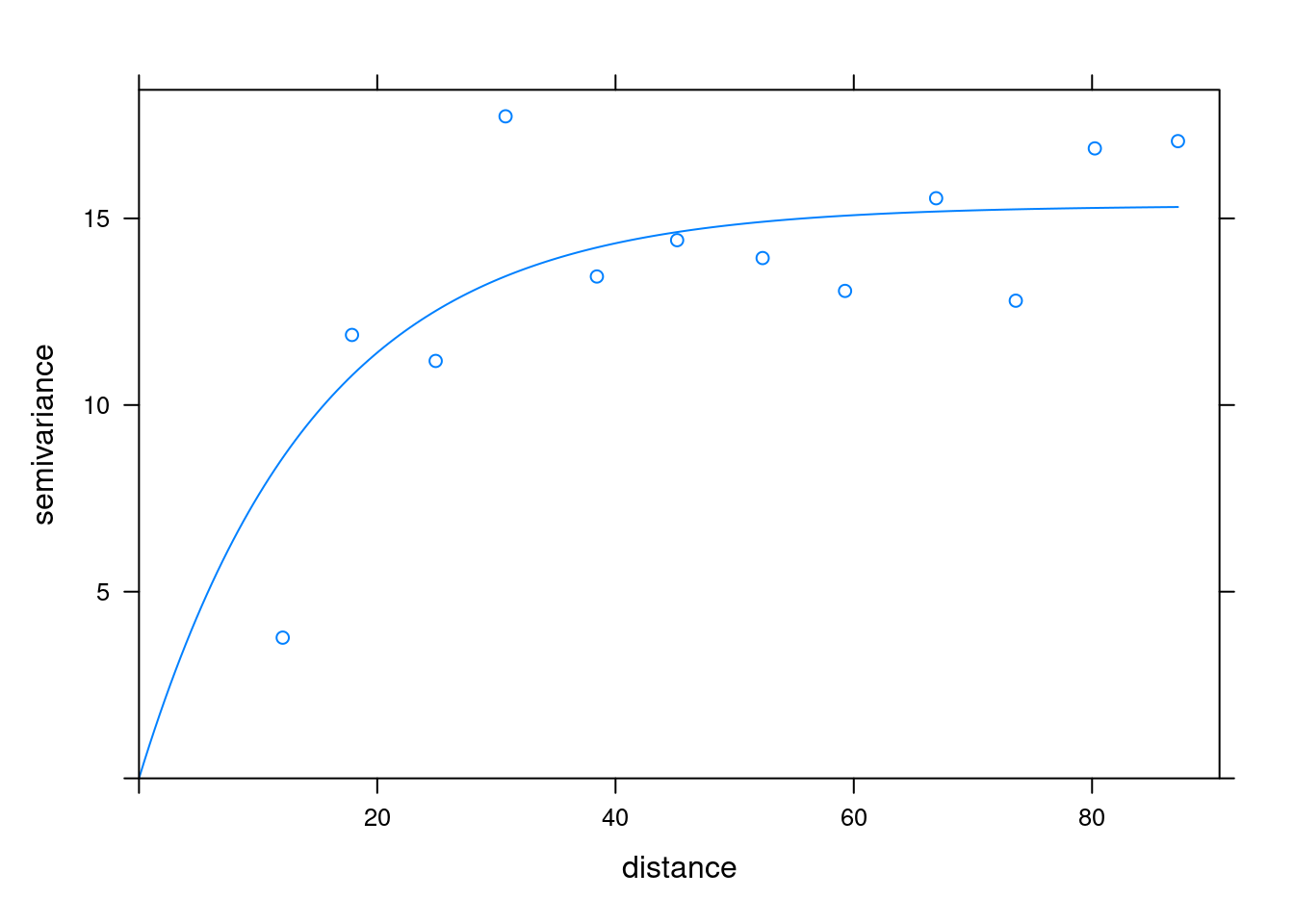
# Modelo Gaussiano
(vmf3 <- fit.variogram(v, vm3))## Warning in fit.variogram(object, model, fit.sills = fit.sills, fit.ranges =
## fit.ranges, : No convergence after 200 iterations: try different initial values?## model psill range
## 1 Nug 0.00000 0.00000
## 2 Gau 14.59874 16.27831print(plot(v, pl=F, model=vmf3))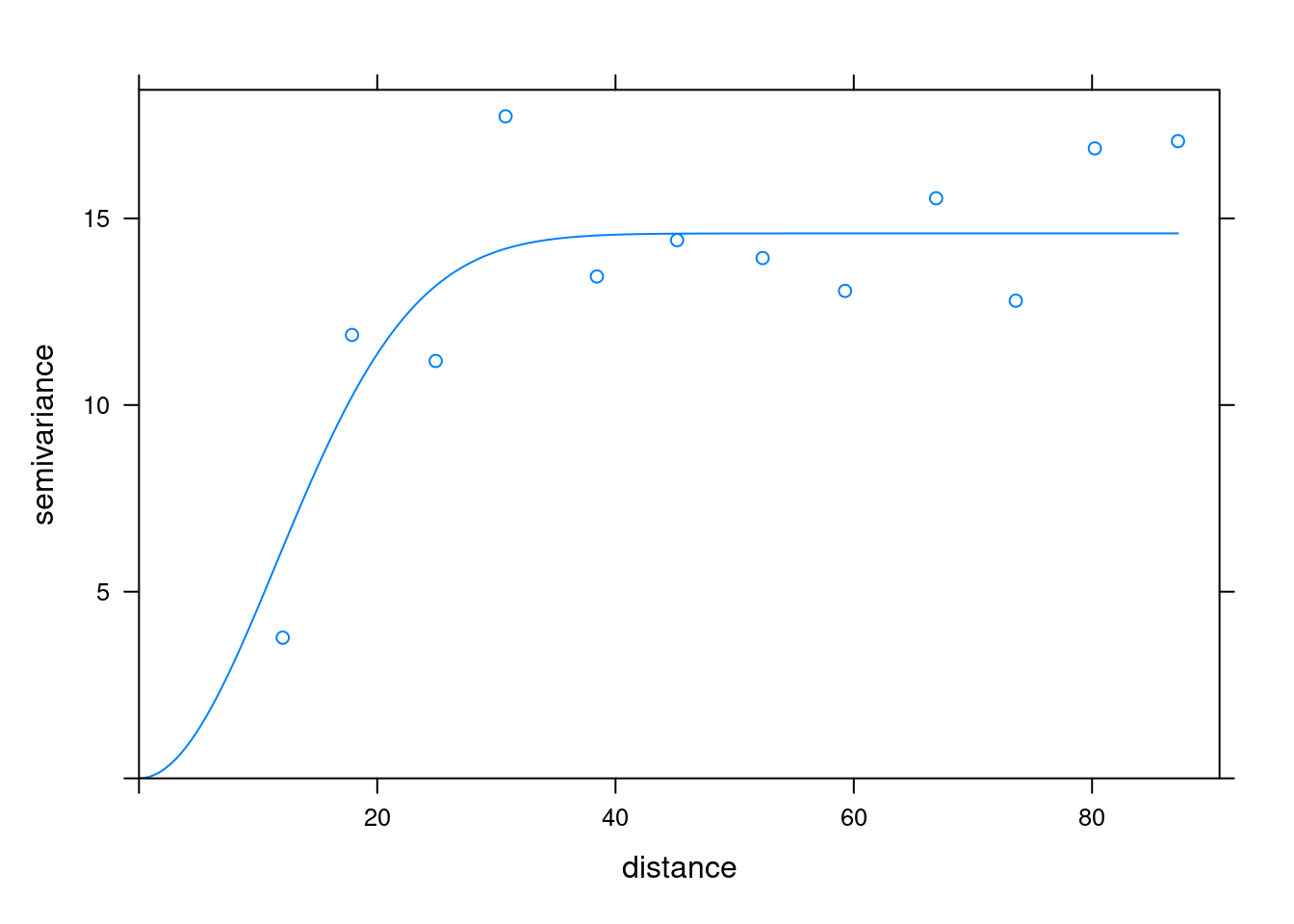 # krigagem
Agora usamos a estrutura espacial para interpolar “de forma otimizada” para os locais não amostrados. Existem muitas maneiras de interpolar; vamos primeiro investigar a krigagem ordinária.
O que há de tão especial na krigagem?
• Prevê em qualquer ponto como a média ponderada dos valores em pontos não amostrados
• Os pesos dados a cada ponto da amostra são ótimos, dado a estrutura de covariância, conforme revelado pelo modelo de variograma (neste sentido o que é “melhor” se ajutou)
• A variação de krigagem em cada ponto é gerada automaticamente como parte do processo de cálculo dos pesos.
# krigagem
Agora usamos a estrutura espacial para interpolar “de forma otimizada” para os locais não amostrados. Existem muitas maneiras de interpolar; vamos primeiro investigar a krigagem ordinária.
O que há de tão especial na krigagem?
• Prevê em qualquer ponto como a média ponderada dos valores em pontos não amostrados
• Os pesos dados a cada ponto da amostra são ótimos, dado a estrutura de covariância, conforme revelado pelo modelo de variograma (neste sentido o que é “melhor” se ajutou)
• A variação de krigagem em cada ponto é gerada automaticamente como parte do processo de cálculo dos pesos.
Krigagem ordinária
Antes de fazer as predições nos grids para geração dos mapas vamos fazer as predições no conjunto de dados de validação para avaliar o desempenho dos modelos.
### Krigando no grid para geração do mapa
## Carregando o limite da área no formato shapefile
limite <- maptools::readShapeSpatial("/home/elias/MEGA/Geo/shape/limite.shp",
proj4string=WGS23S, verbose=TRUE)## Warning: readShapeSpatial is deprecated; use rgdal::readOGR or sf::st_read## Shapefile type: PolygonZ, (15), # of Shapes: 1## Warning: readShapePoly is deprecated; use rgdal::readOGR or sf::st_read## Shapefile type: PolygonZ, (15), # of Shapes: 1### Predicão Exp
grid <- krige(COT ~ 1, locations=data, newdata=grid, model=vm3)## [using ordinary kriging]grid <- raster::stack(grid)
grid = raster::mask(grid, limite)
raster = raster::mask(raster, limite)
tm_shape(limite)+
tm_polygons(col = "lightgrey")+
tm_shape(data) +
tm_symbols(col = "COT", palette = 'YlOrRd', size = "COT", scale = 1.5,
legend.size.show = F, # comment this line to see the original size legend
legend.col.show = T, # comment this line to see the original color legend
title.col="AWC (mm)") +
tm_compass(position = c("center", "top"), size=4) +
tm_grid(alpha = 0.2, labels.size = 1, labels.rot = c(0,90), n.x=5, n.y=6) +
tm_scale_bar(position = c("right", "bottom"), text.size =1) +
tm_layout(title = "", legend.position = c("left", "top"), main.title.position = 'center', legend.text.size = 1)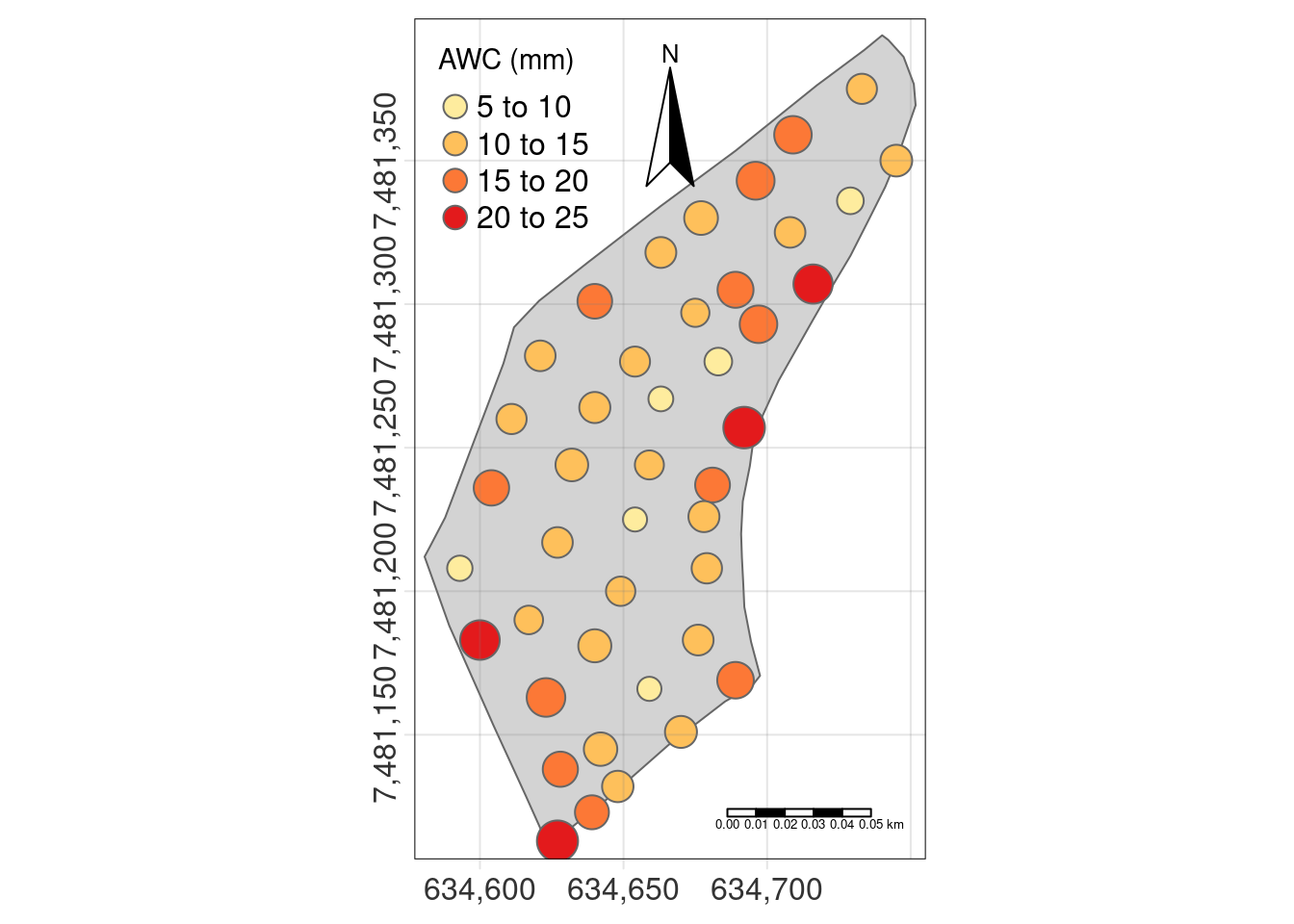
tm_shape(grid$var1.pred) +
tm_raster(title = "COT (g.kg-1)", style = "cont", breaks = c(0,5,10,15,20,25))+
tm_shape(limite)+
tm_polygons(col = "black", alpha = 0, border.col="black")+
tm_compass(position = c("right", "top"), size=4) +
tm_grid(alpha = 0.2, labels.size = 1, labels.rot = c(0,90), n.x=3, n.y=3) +
tm_scale_bar(position = c("right", "bottom"), text.size =1) +
tm_layout(title = "", legend.position = c("left", "top"), main.title.position = 'center', legend.text.size = 1)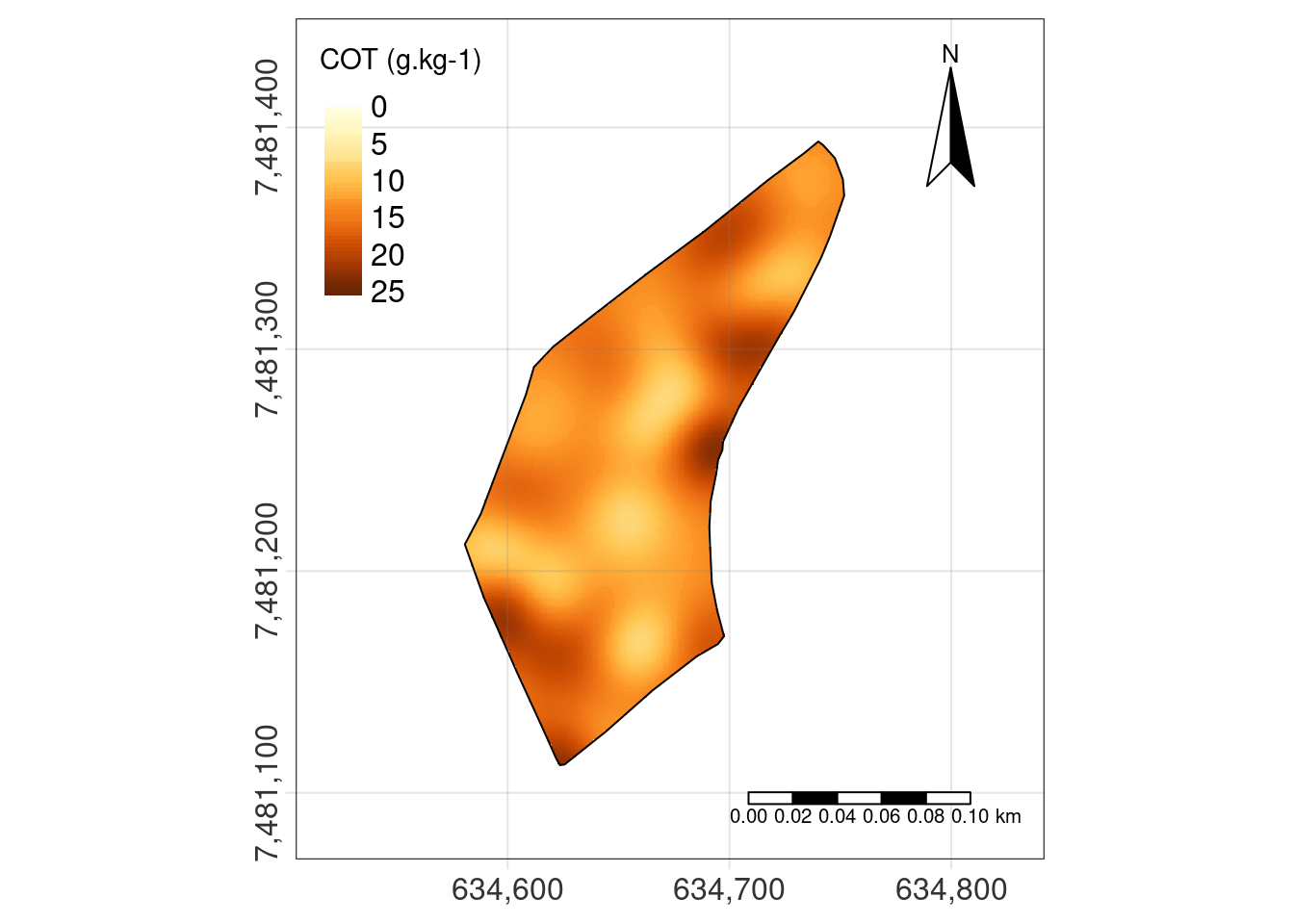
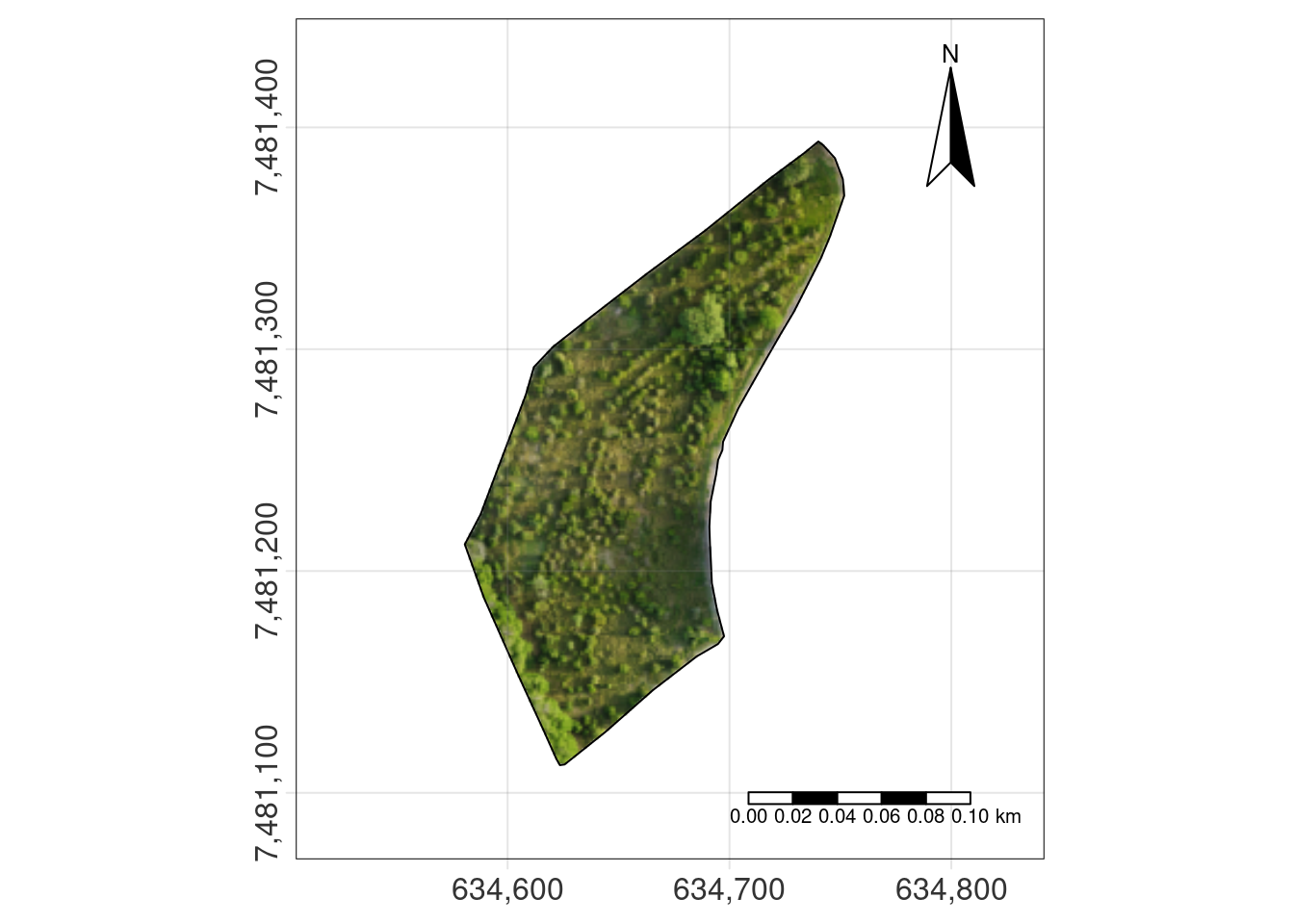
tm_shape(raster) +
tm_rgb(r=1, g=2, b=3)+
tm_shape(limite)+
tm_polygons(col = "black", alpha = 0, border.col="black")+
tm_compass(position = c("right", "top"), size=4) +
tm_grid(alpha = 0.2, labels.size = 1, labels.rot = c(0,90), n.x=3, n.y=3) +
tm_scale_bar(position = c("right", "bottom"), text.size =1) +
tm_layout(title = "", legend.position = c("left", "top"), main.title.position = 'center', legend.text.size = 1)